我要成為單機王──通用遊戲破關之人工智慧方法
組員:陳冠辰、劉承亞、黃迺絜
摘要
在人工智慧的範疇中,強化學習可以解決連續的決策,在遊戲領域中有著很好的應用。目前許多強化學習都是針對特定的遊戲,導入研究者對該遊戲的知識而設計的。而我們的研究則是在不給予機器遊戲規則外的資訊為前提,設計一個可以解決任何遊戲的機器。
介紹
機械學習屬於人工智慧領域,以演算法在大量資料中統計出資料的規則,精準且有效率地實現人工智慧。由於電腦計算效率提升,機械學習目前被普遍運用於許多領域包括電腦視覺、基因定序、自然語言處理、經濟分析、策略遊戲。而機械學習可以用學習方法分成三類。
監督式學習的資料是透過許多組的輸入和輸出,利用演算法和數學模型在數據中學習其中的對應關係,目標是在只有輸入的狀態,預測出正確的輸出。主要應用於統計分類和回歸。統計分類應用很多,例如手寫數字辨識。這種方式就是將輸入資料分類,並以多對一的關係,將各個輸入分別對應到正確的輸出。而回歸分析應用則是利用一對一函數圖形中部份的輸入資訊歸納出一個最符合的預測函數。
非監督式學習與監督式學習的差異在於非監督式學習的數據只包含輸入而不包含相對應的輸出,目標是在這些沒被給予答案的數據中找出共通性。分群演算法就是很典型的例子,其他相同類型的演算法還有資料壓縮與風格變換。
強化學習與以上學習方法有著很大的區別,強化學習目標是在一個環境中,學習出一套策略,取得長遠的最佳回饋。簡單而言他的輸出並不是單純的正確答案,而是會產生解決方案的完整策略。自動駕駛就是其中一個例子,同樣的方法也可以運用到對抗遊戲如圍棋。這些演算法可以在對問題本身沒有先備知識的狀態學習出效果顯著的策略。
背景知識
Reinforcement Learning(強化學習)
(一) Reward
強化學習首先要定義的是reward,目的是讓機器知道學習的目標,而強化學習的目標就是要最大化在和環境互動時取得的reward總和。例如在遊戲中,通關可以定義成獲得正的reward,機器的目標是取得最大的reward總和,因此會盡可能的通關來取得reward。一旦遊戲結束,機器就無法再取得reward,所以機器會盡可能在遊戲結束前通關。
(二) Markov decision process
強化學習可以被定義成Markov decision process,其中包含:
狀態集合 S
動作集合 A
$$ P_{a(s,s^{,})} = P (s_{t+1} | s_{t}, a_{t} = a) $$ 在狀態s下做a會產生s’的機率
$$R_{a(s,s^{,})}$$ 在狀態s下做a產生s’ 所立即得到的reward可取得資訊的規則
(三) Model base / Model free
有些情況下我們可以對環境有充分的了解,知道每個狀態之間的轉移關係,也就是知道Markov decision process的P函數和R函數,這種問題的解法就是Model base。這種情況下可以有一個brute force的方法,枚舉未來的所有狀態所能取得的分數,再選出一個期望值最高的策略。這種方式可以確保有一個正確的策略,雖然可以透過dynamic programming或pruning來降低複雜度,但實際上許多問題狀態組合數很有可能還是太大無法負擔。不過假如我們能夠預估一個狀態未來得分的期望值,我們就可以降低搜尋的深度來取得一個約略的最佳解。
然而現實生活中,有許多問題是無法模擬環境的,因此我們也會希望這類的問題可以有一個不錯的解法,這種解法就是Model free。我們這次的研究目標是在機器完全不知道遊戲規則的情況下通關遊戲,所以需要一個Model free的解法。
Q Learning
Q Learning是一種Model free的強化學習演算法,他會定義一個名為Q Table的表格。Q Table表示每個狀態下每個動作估計可獲得的未來reward總和,假設Q Table是完全正確的,機器可以在每個狀態下查尋該狀態在Q Table中最佳的動作,就可以達到最佳總分。然而我們無法預先取得一個正確的Q Table,因此需要不斷更新修正Q Table,而這個更新即是Q Learning的關鍵。
(一) 定義
(s, a, r, s’) : 表示要更新的資料,從狀態s執行a操作得到r分變成狀態 s’
Q (s_i, a_i) : 即為Q Table,表示在狀態s_i執行a_i操作的未來總分。
alpha : Learning rate常數
gamma : Discount factor常數
(二) 更新
$$ Q(s, a) = (1 - \alpha) * Q(s,a) + \alpha * (r + \gamma * max_{x}Q(s^{,},x)) $$
這種更新方式是透過目前已知的 reward ,加上本身對未來的估計分數,來更新表格。經過重複的更新,Q Table 會慢慢收斂成為準確的估計表格。
(三) Learning Rate and Discount Factor
這裡的learning rate與神經網路的概念一樣,表示每次更新Q-Table的程度,數值越小收斂越穩定,越大收斂越快。而Discount Factor則是乘在對未來的總分估計值上,數值越大代表越信任未來的估計,通常這個參數取決於環境的隨機性,若環境反應較隨機,則需要較小數值。
Neural Network
神經網路是機械學習的方法之一,在五十年前受到生物神經系統啟發而發明,但由於當時電腦計算速度的不足,並沒有很好的成果。而現在隨著電腦硬體速度提昇,神經網路發展快速,也是現在相當普遍的技術。
神經網路是一個數學模型,能將輸入經過一連串的運算,產生出對應的輸出。而在演算法中輸入與輸出通常會被表示成矩陣,而中間一連串的運算即是矩陣的計算,這些矩陣計算也被稱作網路層。網路層是由許多神經元組成,這些神經元是用來將傳入的資料進行一些計算,在傳至下一個接收的神經元。神經元的計算有很多種類,但在計算後都會在套上一個激活函數。激活函數的功用為當類神經網路的數值在傳遞時,將上一層的數值先經過轉化,並將誤差控制在合理範圍內,再傳遞給下一層,這樣可以使輸入與輸出脫離線性關係,以真正實現多層的類神經網路。
輸入層可以視為由只輸出原始資料的神經元組成,輸出層只有輸入最後結果。一個神經網路可以包含很多網路層,當網路層數夠多時,就會稱作深度學習。模型的預測結果會隨著網路層中神經元的計算參數而改變,因此學習的過程就是透過大量的數據,調整這些網路層的參數。
我們可以透過由網路層組成的神經網路,將輸入資料處理成輸出資料,不過這對應關係是各個神經元的參數決定的。對於一組有正確答案的輸入輸出組合,一開始隨機的參數所計算出的結果,很可能與正確輸出不同,因此我們要調整所有的參數,使輸出結果接近正確輸出。這時我們需要得知由模形輸出的結果和正確輸出的差,所以會使用損失函數。例如均方誤差就是一個例子:$$ MSE = \frac{1}{n} \Sigma (Y_{i} - \hat{Y_{i}})^{2} $$
MSE為方均誤差,Y 為模型產生的輸出,Y^為正確的輸出
(一) Optimizer
有了損失函數之後,模型要能根據數據調整神經元的參數,以縮小損失函數的值,這時後會使用優化器。優化器是一些調整參數的演算法,以下以其中的梯度下降法(Gradient Decent)作為說明。
梯度下降法十分直覺,可以把損失函數對應到一個空間,維度是參數數量加一,我們要在這個空間中找到一個點使的函數的值最小,那他的座標就會是這些參數的最佳解。要減少損失函數的值,可以不斷的朝凹處移動一小步。
實際上的作法是對於每個參數(也就是每個維度)把損失函數對其偏微分,得到的梯度代表的方向是上坡的方向,要減少損失函數便要向負的梯度方向調整一些距離。一些距離則是決定於 learning rate。
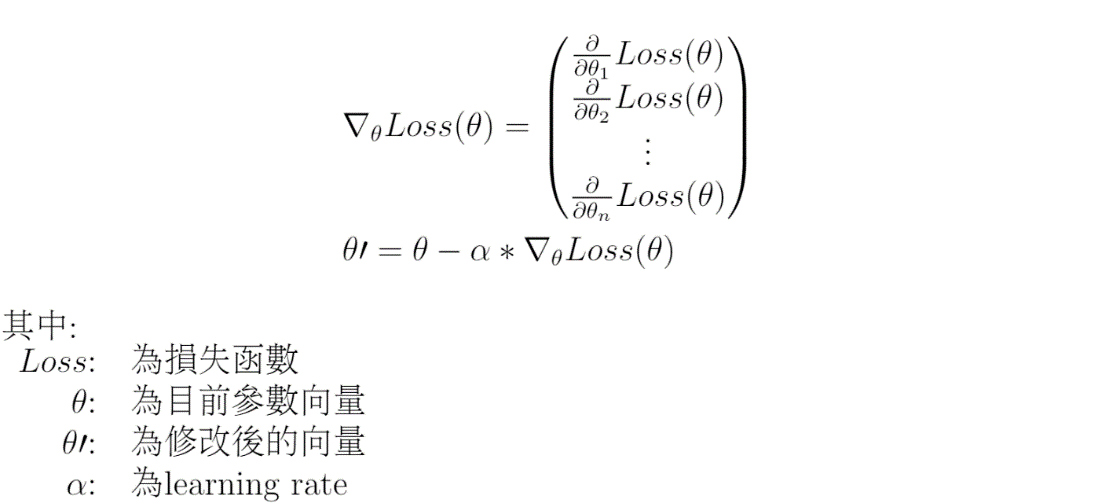
在持續的調整參數之後,損失函數有機會停留在一個區域的極小值。可以注意到的是梯度下降法不能保證解出整個函數最小值,這是因為損失函數可能不是凸函數,所以不斷朝向低處走得結果只會是區域極值。所花的調整次數取決於 learning rate,過大的 learning rate 會調整過當,無法停留在極值。過小的 learning 需要花很多次調整才能達到極小值。參數停留在區域極值而變化不大,即為收斂。
Deep Q-Learning
Q Learning 在理論上能夠透過反覆更新 Q Table,收斂達到很好的效果。但實際上 Q Table 大小為狀態數和操作數的乘積,這在一些簡單的環境下是可以被更新完成的。而我們的實驗目標是要讓機器對於輸入的一張圖片決定出相對應的動作,我們的狀態量對圖片大小就會是指數量級成長,導至無法在有限時間內更新完成。有一種解決方式是透過影像處理,辨識出主角、物件、敵人所在位置,大量降低 Q Table 複雜度。雖然這種方式有效,但依賴人類的知識,以及對每個遊戲的獨立處理,不是我們的研究範疇。
另一種方式是在強化學習上搭配神經網路,透過與環境的互動訓練神經網路,使神經網路能擷取圖片的抽象資訊,來降低Q Table複雜度。圖片的輸入常使用捲積神經網路,這種網路是啟發自動物的視神經,能夠透過訓練,學習擷取圖片局部特徵。實做上就是把Q Table以神經網路取代,該神經網路的輸入是圖片,輸出則是與操作集合有一樣大小的矩陣,每個元素代表該操作的Q Table值。更新則是用和原本Q Learning一樣的式子,配合Loss Function,使用梯度下降法更新。另外再使用Memory replay與Double Q Learning的技巧優化,達到更好學習效果。
研究動機
我們這組對於人工智慧十分想要一探究竟,在學習了與其相關的知識後,便想要借助人工智慧的力量,打造一個能破關所有遊戲的程式。
研究目的
透過這個實驗,我們希望能用Deep Q-learning以model free的模式,來通關一個單機遊戲,進以推廣到所有圖像處理的問題。
實驗器材及裝置
我們所使用的語言是python 3.7,而神經網路的部份是使用tensorflow的keras套件所建造的,而我們所使用的遊戲環境是Open AI裡的AI gym專案。而我們所選擇的遊戲是Cartpole,他是一個平衡棍子的遊戲,用Deep Q-learning以model free的方法,來通過這個遊戲。
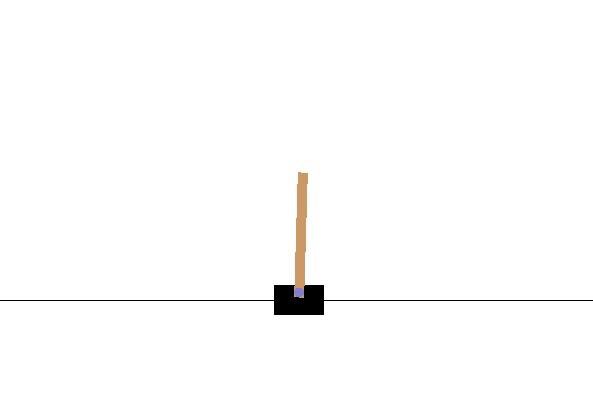
這裡先介紹一下Cartpole是一個怎麼樣的遊戲。如上圖所示,就是一台車子(Cart)上有一隻竿子(pole)。而車子每移動一單位的距離,分數就會加1。當竿子跟垂直方向差超過15度時,遊戲就會結束。
研究過程及方法
一開始我們所預想的是希望能夠使機器透過輸入並讀取圖像來計算棍子當前的速度與方向,並且學習如何攻略遊戲。但過程中遇上問題,我們圖像處理的計算速度緩慢,效率不佳;而儲存學習結果的空間也遇上麻煩。所以後來透過改變機器的輸入,從圖像轉變成獲得速度與方向來學習,進以實驗Deep Q-learning配上model free這個方法在遊戲上的表現。
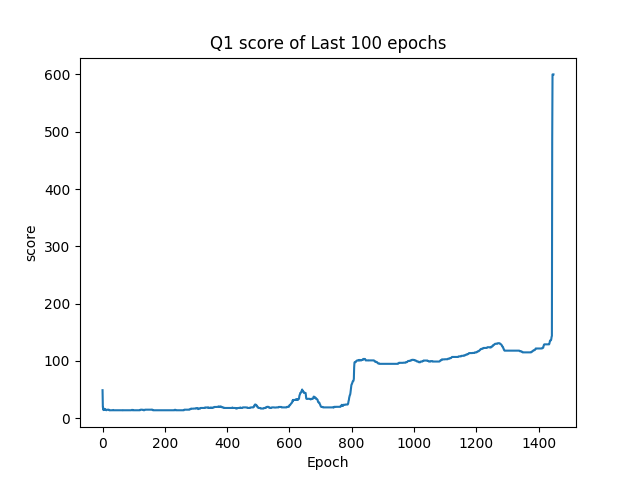
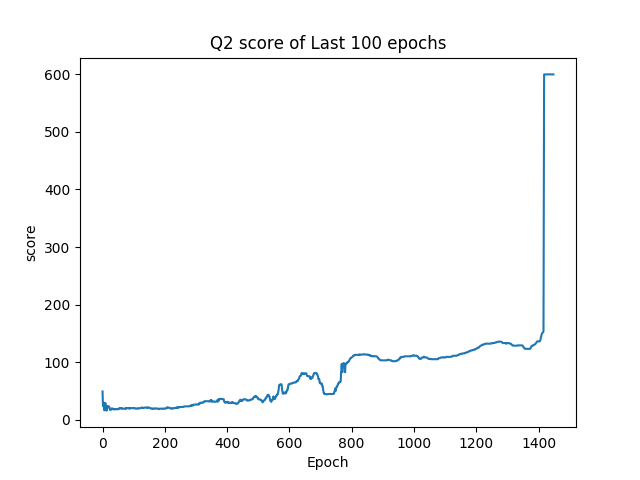
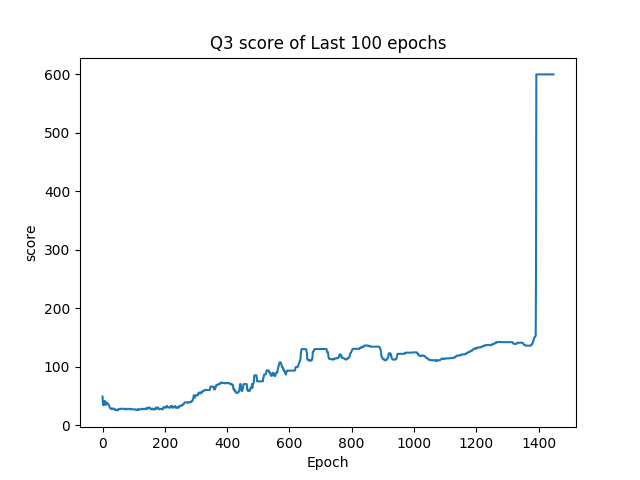
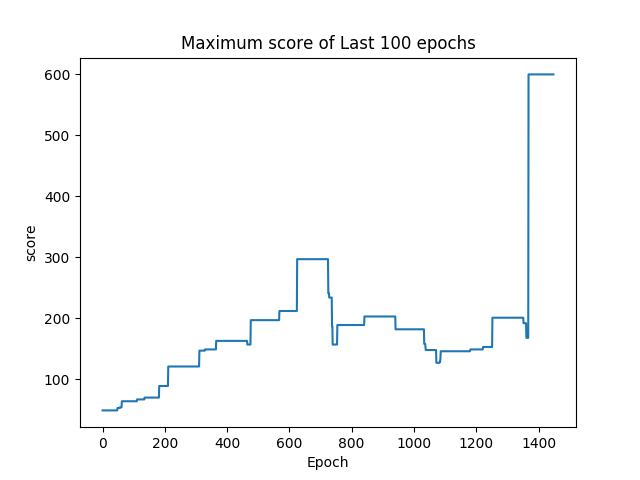
我們每100局遊戲會紀錄這100局遊戲的結果,分別紀錄分數的平均值、四分位數、以及最大值還有神經網路學習狀態的loss值。紀錄loss值的原因是,如果神經網路的學習到最佳了,那麼強化學習的部份也應該要學習到最佳,所以loss值就能夠看出我們人工智慧的學習狀況。而在單局內如果分數超過600分,就會停止遊戲,因為這樣極有可能是竿子已經達到平衡狀態,遊戲是不會停止的。
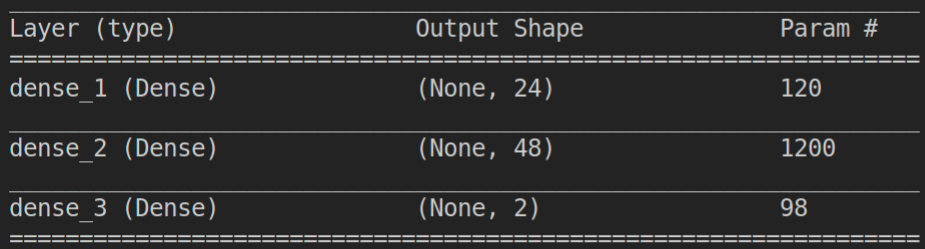
在神經網路的部份,由於輸入圖片運算速度太慢,所以改為輸入當前竿子的方向與速度。而對於計算數值所使用的神經網路是Dense,若運算設備足夠完全,輸入的是圖片時,用CNN基本上也是可以運作的,只是目前無法以實驗證明。CNN較為Dense複雜,運算速度也相對比較慢,而數值不像圖形有所相近的關聯性,所以採用Dense的效益大於CNN,所以實驗就使用Dense。
在神經網路的部份有三層,使用了tanh和linear的激活函數,而所使用的loss函數是均方誤差函數(MSE),優化器則使用Adam。
Q learning所使用的learning rate為0.02,discount factor為1,用1的原因是,這個遊戲不是隨機的,所以操作都應該要按照他所學到的執行。而我們有採用一個學習策略叫做epsilon-greedy。由於學習一開始的能力較弱,所以需要一個隨機的操作,而這個策略就是要告訴模型要有多少比率的操作要是隨機的。而學的越久,模型也會隨之增強,所以隨機的比率就要越來越低。使用了一個常數epsilon,介於0到1之間,代表多少比率的操作要隨機,而他會隨著epsilon-decay-function減少。(epsilon_decay = 0.007在第1000回合epsilon會等於0.001) $$ epsilon-decay- function(\epsilon) = max(0.001,1 - log_{10}(\epsilon * 0.007))$$
研究結果
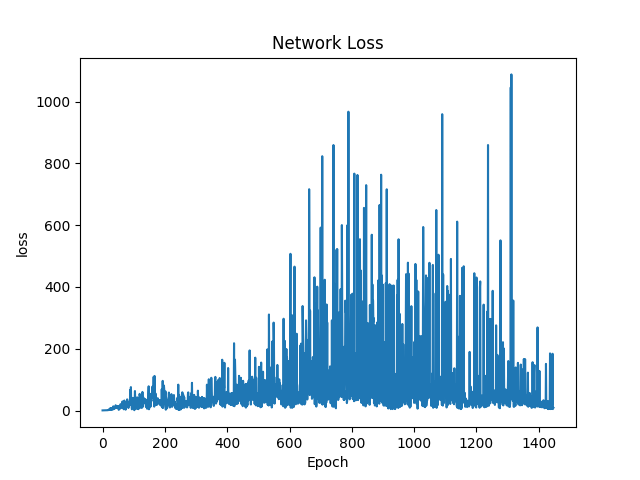
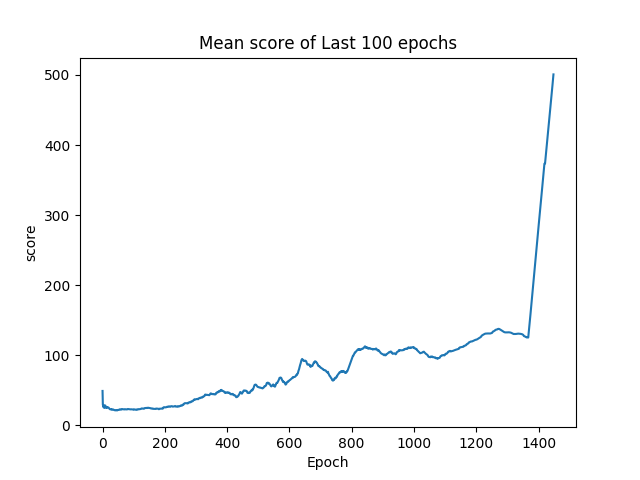
討論與結論
由研究結果中的(圖一)可以發現loss function的值在最初是較低的,這是由於剛開始程式對於遊戲並不熟悉,因此在幾乎接近隨機操作的情形下,無法有效尋找正確的方向。因此此時loss function的值並非當時與正確結果之間的差異,而是程式錯誤的估計。若按照與理想目標之間的差距作圖,應該為一個負相關的圖。
由(圖二)到(圖五)可以得知整體趨勢為正相關,因此可以得知在資訊量小的情形下,此方法是可行的。當資訊量較為龐大時,則需要利用CNN捲積神經網路先將資料抽象化及簡化,但礙於目前所使用之硬體設備算力不夠,捲積神經網路是否能有效收斂以及其與Deep Q-Learning之間是否能有效配合還未得到證實。
未來展望
能夠透過直接讀取圖檔來進行遊戲通關,進而驗證我們的方法。
能夠自主訓練需要互動的問題,如對局遊戲等。
希望訓練出來的模型能在相同類型的遊戲上有效的轉移,以節省訓練模型的時間。
參考資料
2016 OpenAI (https://openai.com) OpenAI Gym