「醇」「醇」欲動──探討丙二醇液滴的馬蘭哥尼效應
組員:葉芳瑜、謝亞彤、謝秉希
摘要
本實驗探討不同濃度醇類液滴在載玻片上的交互作用現象「馬蘭哥尼效應」。我們以火焰燃燒15秒、載玻片懸空19公分代替電暈表面處理,並進行一連串實驗與分析。實驗發現欲使兩液滴產生互相推拉的運動,兩液滴間須保持一最小表面張力差值為3 dynes/cm;又表面張力差越大,液滴運動的加速度越大,表示液滴移動愈快,從錄影紀錄也能清楚看見。此外我們也發現了「混合區」的存在,並確定其與兩液滴交互作用的關係。利用比爾定律計算出混合區的濃度,可發現與我們所得之表面張力最小極限值相符合,藉此找出液滴停止推拉現象之成因。
透過上述研究結果,設計出改良式的選色實驗(sorting experiment),以階梯式取代等長式液滴層,並選用1%、5%、15%、25%、40%與60%的丙二醇液滴,成功讓七彩液滴在載玻片上舞動。

圖1 階梯式選色實驗
研究動機
在Stanford News於2015年3月發表的影片中,有一影片為「Mystery of the dancing droplets」,呈現不同濃度丙二醇的液滴在電暈表面處理(corona treatment)的載玻片上牽引、推動的交互作用,實驗中液滴經色素染色後不僅更有利於觀察,也增添視覺上的美感,顯得格外引人注目。由於影片甚少提到實驗背後的原理,我們搜尋文獻、網路資料,才得知此現象稱為「馬蘭哥尼效應」(Marangoni effect)。此效應指在流體介面,因表面張力梯度而造成的傳質現象,在日常生活或工業廣泛應用,但實際原理並不清楚易解,影片中的被動選色實驗(sorting experiment)或稱階梯實驗看似簡單,但經初步嘗試後,我們發現成功率不高。為了完美重現此實驗,我們設計一系列的研究。首先我們想探討不同藥品的水溶液是否能呈現與丙二醇相似的馬蘭哥尼效應,也嘗試調整醇與水的濃度,觀察液滴運動的快慢,並進一步探討導致液滴交互作用停止或混合的原因,推測兩液滴交界處存在一狹窄的「混合區」,兩液滴會在此區進行物質傳遞。藉由研究物質傳遞的多寡與相對濃度,並推論濃度與表面張力的關係,我們想印證維持兩液滴交互作用所需最小的表面張力差值,找出產生馬蘭哥尼效應的必要條件。
研究目的
(一)設計實驗系統模組
(二)研究不同有機溶劑是否能產生馬蘭哥尼效應
(三)研究不同濃度之溶液間的馬蘭哥尼效應有何異同之處
(四)設計被動選色(sorting experiment,或稱階梯實驗)之機制
(五)探討溶液混合或停止追逐現象之成因
實驗方法
馬蘭哥尼效應
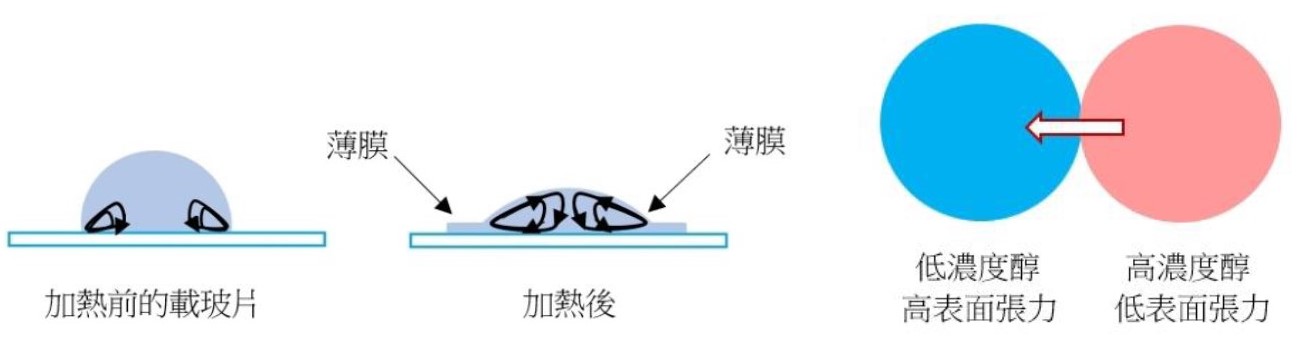
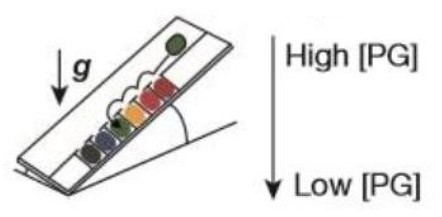
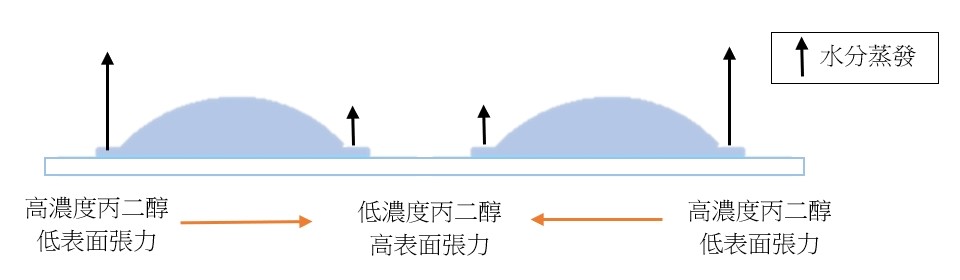
馬蘭哥尼效應是由於流體介面的表面張力梯度(gradient of surface tension)所造成的傳質現象。造成表面張力差異的變因包含溫度與界面活性劑,如清潔劑。當載玻片的溫度經加熱提高後,其表面能會增加,增加其潤濕性與附著力,使液滴接觸角變小。此液滴與載玻璃接觸面積較大,同時液滴自身的表面張力使其產生回縮的趨勢,因此液滴邊緣的溶液較薄,即「薄膜」(thin film)。(圖二)此區的較大表面積使蒸發對溶液影響加劇。水的表面張力較醇類溶質高,蒸發速率也較快,所以在薄膜中,醇類的濃度較高、表面張力較小,整顆液滴的不同區域因而有表面張力的差異,相對邊緣區域,液滴中央的表面張力高於邊緣區域,溶液會從低表面張力流至高表面張力的區域,由外側底部沿著表面往上流動,即馬蘭哥尼流。 當兩顆液滴在一定距離內,兩顆液滴會就表面張力的差異而產生追逐或相吸的現象。 第一種情形是當兩顆液滴丙二醇的濃度相同時,它們會互相吸引直到匯聚成同一顆液滴。因為兩顆液滴中間的水分蒸發量因蒸氣聚集而較兩側少,因此此區水分濃度高,所以表面張力也較高,吸引溶液流向此。另外一種追逐的情形則發生在兩顆液滴的表面張力達一定差值時,高表面張力會吸引低表面張力的液滴,造成貌似追逐的現象,也就是高濃度會朝低濃度醇類水溶液液滴靠近。
設計實驗系統模組
(一)實驗流程與裝置
實驗流程可分為下列步驟:

為控制每一片載玻片的溫度,本生燈的火焰高度(火焰的上端)設置在20公分,載玻片的懸空高度為19公分(如圖五),加熱的時間固定為15秒。加熱完畢後,載玻片需靜置待其溫度降回室溫。

如圖六所示,我們使用微量吸管吸取溶液,使每次實驗之液滴大小控制在10ul。每一組實驗的兩液滴之間距為1公分(以液滴中心計算)(如圖七)。
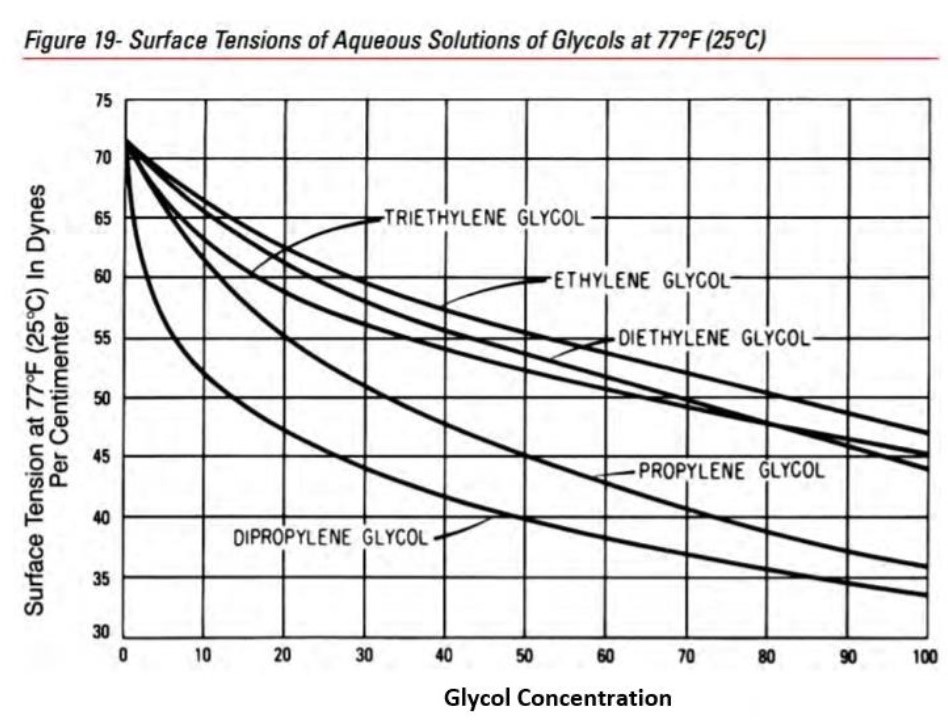
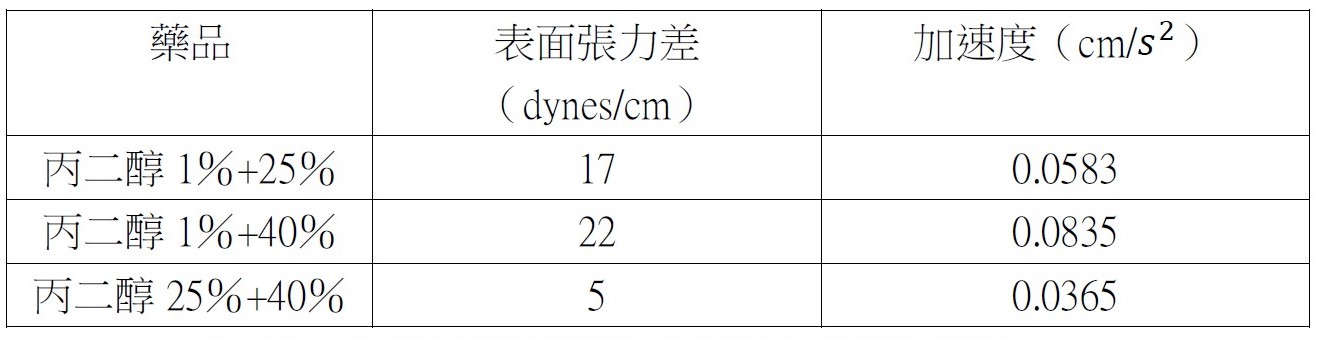
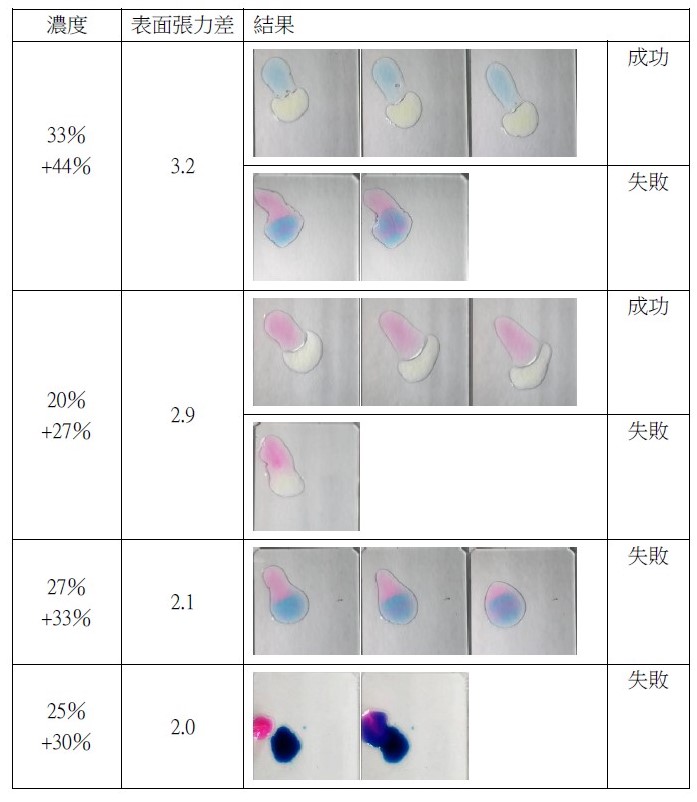
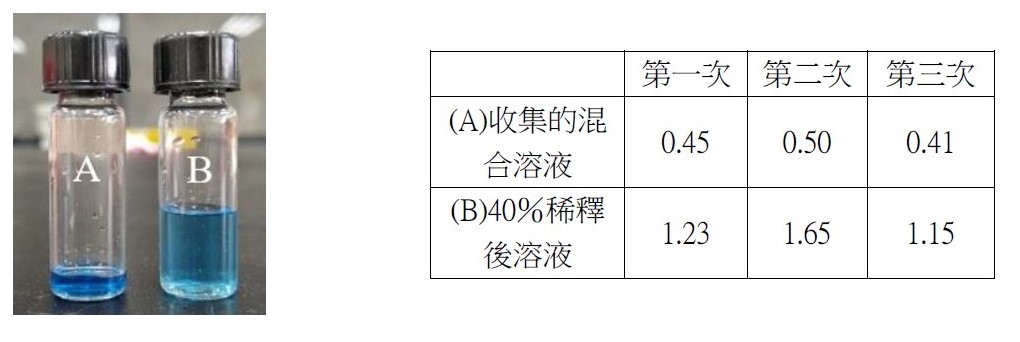
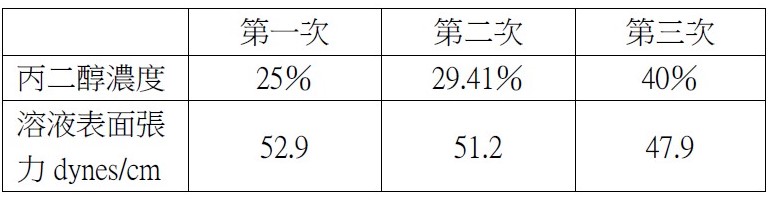
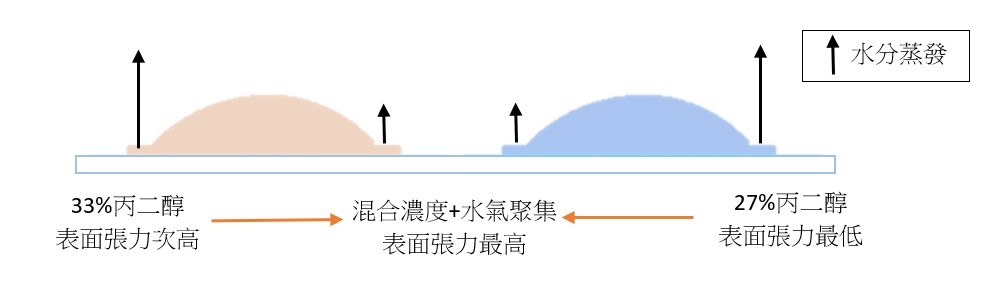
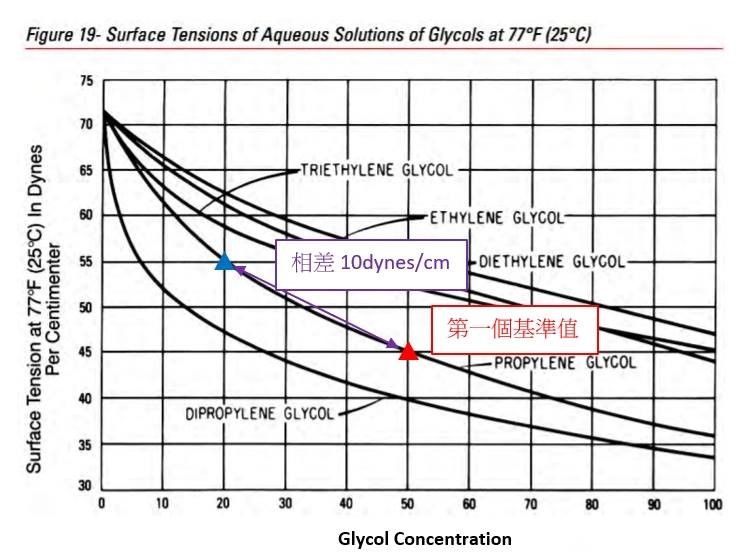
如圖八所示,我們放置攝影機,以記錄實驗結果,同時在手電筒提供光源的情況下能更清楚觀察液滴移動的情形。 (二)實驗結果成功或失敗之定義 不同種狀況下會產生不一樣的液滴互推結果,為使討論方便,我們定義了實驗成功或失敗如下: 建立實驗系統後模組後,我們欲探討除了丙二醇之外,其他藥品是否能成功呈現出馬蘭哥尼效應。因此我們以同為醇類的乙醇、乙二醇與正丙醇進行實驗,也選用同為有機物的乙酸。 (一)不同濃度之實驗結果 藉由改變兩滴液滴的濃度,我們欲探討濃度對馬蘭哥尼效應的影響。我們先選擇1%、25%與40%的丙二醇水溶液進行實驗。並透過Tracker程式分析液滴的移動狀態和計算。 根據牛頓第二運動定律, $$ F = ma $$ 影響液滴加速度的關鍵為其受力大小。又由原理得知馬蘭哥尼效應的重要變因之一為液滴的表面張力差。因此能進一步推論濃度迥異導致的表面張力差與液滴受力大小的關係。 (二)探討所需最小表面張力差 由馬蘭哥尼效應的原理得知,液滴移動是因兩者之間存在足夠的表面張力。經實驗1%、25%與40%三種濃度後,可發現其都能產生穩定的馬蘭哥尼效應。我們假設若繼續改變濃度,以縮小液滴間表面張力差值,最後能找到使實驗成功的最小表面張力差極限值。於是我們設計了以下實驗: 為了確定丙二醇溶液在不同濃度時的表面張力,我們尋找了國外的文獻資料,且用座標法去計算,圖表如下圖: 實驗結果若成功,我們就再次縮小液滴的表面張力值,直到實驗結果失敗。 我們改良文獻中的被動選色機制(圖十一),根據目前實驗所得數據,重現實驗動機所提的影片實驗。並同樣以座標軸算出不同濃度的表面張力,並找出適合進行實驗的六種濃度差 由原理得知,馬蘭哥尼效應,是源於兩液滴之間存在足夠大的表面張力差,在實驗三–(二)中,我們也找出表面張力差的最小極限值。 實驗中,兩液滴的交互作用並非永恆,液滴最後會停止移動或混合。若兩液滴的表面張力差持續存在,兩液滴應可以永遠維持交互作用,然而實驗結果並非如此。 透過此現象,我們推測液滴在推動的過程中,其交界處存在一「混合區」。兩邊的液滴將於此混合區交換溶液,最終使得兩液滴的濃度隨著移動的時間改變。在過程中,低濃度的液滴濃度會逐漸升高,使得前後兩液滴的濃度差越來越小,表面張力差也越來越小,當其量值小於我們所計算出的最小極限值時,兩液滴的表面張力差即不足以維持交互作用,而造成液滴停止推動與混合的現象。 為了印證此假設,我們設計以下實驗: (一)驗證混合區的存在 若採用原先實驗操作,兩滴液滴以不同色素染色,如黃色和藍色,會因微量混合使顏色變化不易清楚辨別。因此我們選擇以沉澱反應替代: 碘化鉀和硝酸鉛反應後會產生黃色沉澱物碘化鉛,若將碘化鉀和硝酸鉛分別配製在不同濃度的丙二醇溶液中,就能觀察到液滴在運動過程中是否有混合。 (二)分析混合區濃度 由上述沉澱實驗,我們確知在運動過程中,會有部分溶液混合,因此我們設計下一步實驗,分析兩滴液滴混合前,混合區的丙二醇濃度。 若有一杯色素量固定(顏色深度不變)的高濃度溶液與另一杯透明無色的低濃度溶液混合,會得到一杯新的混合溶液,其顏色因色素濃度被稀釋而變淺,丙二醇濃度也介於高濃度與低濃度之間,我們就能藉顏色的變化來推得混合溶液的濃度。 在實際操作實驗時,一滴為無色的較低濃度丙二醇水溶液,另一滴則為色素染色後的較高濃度丙二醇水溶液,在運動過程中,前面的無色液滴為低濃度,後面則為高濃度且經過染色,所以在液滴運動進行物質傳遞的同時,前面的顏色因色素濃度增加會逐漸加深,也就代表其丙二醇的濃度提高。 在兩液滴混合前以微量吸管吸取混合區的溶液,應用比爾定律(Beer's law)比色,便可知其色素相對濃度並進一步推出兩滴液滴完全混合前丙二醇的濃度。比爾定律為光吸收定律,當光通過一介質後,介質會吸收光束而減少光束強度。當此介質的濃度愈大、厚度愈大,則光強度的減弱會愈明顯。 當一束平行單色光垂直通過某一均勻非散射的吸光物質時,其吸光度 A 與吸光物質的濃度c 及吸收層厚度l 成正比。其關係式為: $$ A = k \times l \times c $$ k:係數,為衰減係數或莫耳吸光係數,l:吸收介質的厚度,一般以 cm 為單位,c:吸光物質的濃度,單位可以是 g/L 或 mol/L 實驗流程: 本生燈火焰高度:20公分,液滴大小:10,玻片高度:19公分,液滴間隔:1公分 研究結果: (一)不同濃度之實驗結果 由實驗結果可整理出: 由上表和上圖我們皆可清楚觀察到液滴的加速度確實與兩液滴間的表面張力差呈現正相關的趨勢,也可推測表面張力差越大,液滴所受的力越大。 (二)不同濃度差之實驗結果 第一次: 第二次: 第三次: 當實驗至濃度40%對50%時,表面張力差值只剩約為3 dynes/cm,我們發現實驗成功率大幅降低,因此我們推測此數值應逼近表面張力差的最小極限值。接著我們將表面張力差值再縮小到2 dynes/cm。 第四次: 濃度44%對50%經多次實驗後,結果皆為失敗,因此我們推測要使實驗成功確實存在一表面張力差的最小極限值,約在3 dynes/cm左右。 為了印證我們的假設,我們又找了另外三組不同的濃度,表面張力差值各為2和3 dynes/cm,來進行實驗: 可見當表面張力差值接近3 dynes/cm時,實驗雖會有可能會成功也會失敗,而表面張力差值接近2 dynes/cm時必定失敗。故最小表面張力差極限值約為3 dynes/cm。 實驗結果: (一)驗證混合區的存在 實驗結果: 透過實驗可以發現在液滴運動時,兩液滴交界處確實會出現黃色沉澱物,也就證明了兩液滴雖看似不混合,但仍有少量的溶液會從後面的液滴進到前面的液滴,「混合區」確實存在。 (二)分析混合區的溶液濃度 原高濃度溶液與混合溶液圖片如圖十四,使用比爾定律比色結果為表十二。 由比爾定律 $$ A = k \times l \times c $$(k:係數,為衰減係數或莫耳吸光係數;l:吸收介質的厚度(cm);c:吸光物質的濃度(g/L)),可知在兩瓶溶液顏色相同的情況下,其高度與濃度成反比。 三次結果的算術平均值為29.41%,代表混合區的丙二醇濃度為29.41%,查照圖十其表面張力為51.2 dynes/cm。 在兩液滴混合前一刻,混合區溶液與後面高濃度液滴的表面張力差值約為3.3 dynes/cm,逼近我們在實驗三–(二)所量測出的3 dynes/cm,因此不足以維持兩液滴的交互作用。 在原文文獻中,載玻片經過電暈處理,意即利用高頻率高電壓使欲處理的非導體表面電暈放電,使其產生低溫電漿。這些帶電粒子藉由電擊和滲透破壞物體表面的分子結構,將其表面分子氧化和極化,增加表面的潤濕性與附著力。 由於我們不具備電暈放電(corona discharge)的技術,所以我們選擇火焰處理。其原理是在以本生燈燃燒載玻片時,火焰燃燒產生的氧自由基、碳分子等會破壞附著在載玻璃表面的長鏈分子結構。從微觀角度來看,載玻片的表面會變得比較粗糙,因而增加載玻片對液滴的附著力。 未經燃燒的載玻片有較差的潤濕性,其上的液滴接觸角較大(圖十五),相比之下,燃燒後的載玻片有高表面能,使液滴較易附著 (圖十六),利於實驗進行。 經實驗乙醇、乙二醇、丙二醇、正丙醇、和乙酸後,以上都能產生馬蘭哥尼效應。根據實驗原理,馬蘭哥尼效應的原動力是表面張力梯度,在液滴薄膜中,因較大的表面積會使蒸發量對液滴影響加劇,我們認為,只要此物質與水的蒸發速率有差異,就會造成表面張力不均勻,而產生馬蘭哥尼效應。由於此五種有機溶劑中,丙二醇的實驗效果最佳,液滴交互作用的情形最易觀察,故往後皆以丙二醇來進行實驗。 液滴之所以會運動,是由於表面張力差所致。已知相同丙二醇濃度的兩滴液滴會產生如圖十八的交互作用。在兩液滴之間的薄膜內,因水氣聚集影響,水分的蒸發量會較外圍區少,此區水分含量因而相對高,表面張力也較高(水的表面張力大於丙二醇表面張力),因此液滴會持續接近彼此,直到混合為一體。我們認為當表面張力差小於臨界值3 dynes/cm時,兩滴液滴的丙二醇濃度十分相近,兩液滴之間的表面張力大於兩者之中較低濃度的液滴,因此也會停止追逐運動而互相接近並混合。 圖十八為一次失敗實驗所使用的丙二醇濃度,當混合區的表面張力有系統中最高的表面張力時,在表面張力梯度的作用下,兩邊液滴會互相靠近,直到最後混合在一起。 我們先選擇一固定濃度(50%)作為基準值,並利用圖十一計算出基準值的表面張力,再利用與此溶液表面張力相差10dynes/cm的丙二醇溶液(20%)開始實驗。 實驗可行後我們欲改變丙二醇濃度以降低兩液滴的表面張力差,為了實驗方便性,我們會以上組實驗時兩濃度之一的丙二醇溶液作為基準值,再利用同樣的圖十一查出接續欲實驗的張力差值所對應的濃度,同時確保此濃度值易於配製。 最後我們對回圖十,找出另一組張力差相等的溶液作為驗證組。 實驗動機提到的影片中,原實驗區隔不同顏色液滴的黑色簽字筆線為等長式,如圖二十所示 經嘗試後,我們認為等長式不適合被動選色機制,第一,因油性簽字筆的性質易被醇類溶解,所以液滴無法靜止在簽字筆層而會直接流過;第二,不同濃度的液滴間會存在引力,使其無法靜止於每一層中,第三,如圖二十所示,直線式不易讓下滑液滴與各液滴接觸,所以我們決定改良成階梯式 (圖二十一) ,每一層較上層突出0.5公分,因此階梯式能克服上述問題,又因每一滴下滑液滴可以輕易的掉入每一層中,所以不同濃度間液滴推動的現象能清楚看見。 液滴下滑的原動力為重力,實驗中載玻片以右下角為支點,向右下傾斜,每次實驗我們皆固定傾斜角度(14度),使液滴能以適合的速率下滑。若向下傾斜的角度太小,液滴的下滑速率就會因太慢而其與層間液滴的交互作用時間拉長,導致溶液傳遞過多,使原濃度值偏差,造成實驗失敗。 一、同為有機溶劑的乙醇、乙二醇、正丙醇、與乙酸實驗結果都會成功產生馬蘭哥尼效應。乙二醇與乙酸所呈現的視覺效果與丙二醇一樣好,而乙醇與正丙醇則因本身表面張力太小使高濃度溶液散成薄膜。 二、不同濃度溶液間要產生相似的交互作用存在一表面張力差的最小極限值,約為3 dynes/cm,而當兩種濃度溶液間的表面張力差越大時,液滴運動的加速度越大,所以液滴運動的也越快。 三、丙二醇溶液濃度分別為1%、5%、15%、25%、40%與60%,並採用階梯式,能產生成功的被動選色機制(sorting experiment)。 四、液滴交互作用時,交界處確實存在一「混合區」。 五、液滴停止交互作用的原因是因為混合區的存在使其進行物質傳遞,低濃度液滴的濃度因此逐漸上升,最終因表面張力差不足以維持獨立的兩液滴而混合。 Tom Abate, Stanford researchers solve the mystery of the dancing droplets Stanford Report Retrieved March 11, 2015 from https://news.stanford.edu/news/2015/march/dancing-droplets-prakash-031115.html Takamura, K., Fischer, H., & Morrow, N. R. (2012). Physical properties of aqueous glycerol solutions. Journal of Petroleum Science and Engineering, 98, 50-60. Marangoni effect from https://en.wikipedia.org/wiki/Marangoni_effect Corona treatment from https://en.wikipedia.org/wiki/Corona_treatment 國立台中教育大學科學遊戲實驗室•水滴之舞•取自http://scigame.ntcu.edu.tw/water/water-024.html Cira, N. J., Benusiglio, A., & Prakash, M. (2015). Vapour-mediated sensing and motility in two-component droplets. Nature, 519(7544), 446. Beer–Lambert law https://en.wikipedia.org/wiki/Beer%E2%80%93Lambert_law Flame treatment from https://en.wikipedia.org/wiki/Flame_treatment



研究不同有機溶劑是否能產生馬蘭哥尼效應
研究不同濃度溶液間的馬蘭哥尼效應有何異同之處
設計階梯實驗之機制
探討溶液混合或停止追逐現象之成因
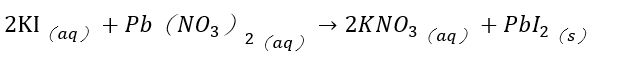

實驗結果
設計實驗系統模組

研究不同有機溶劑是否能產生馬蘭哥尼效應

研究不同濃度之溶液間的馬蘭哥尼效應有何異同之處


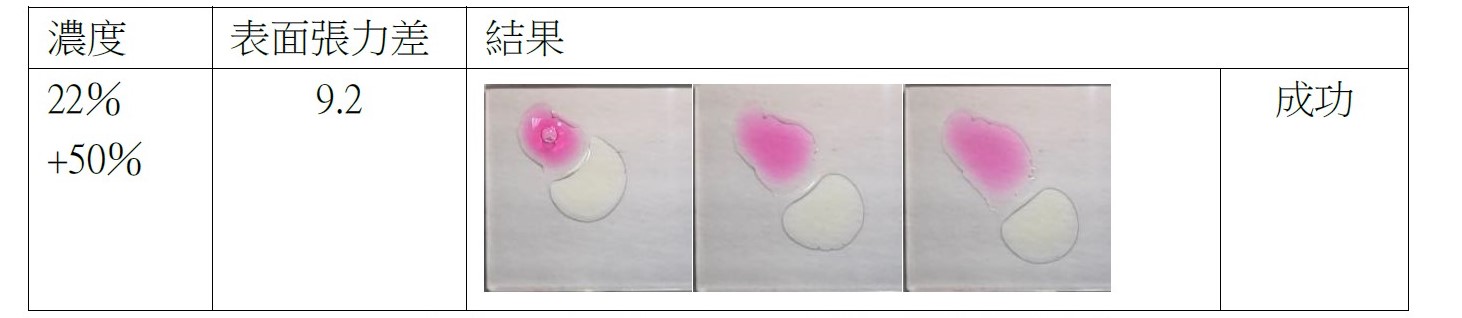
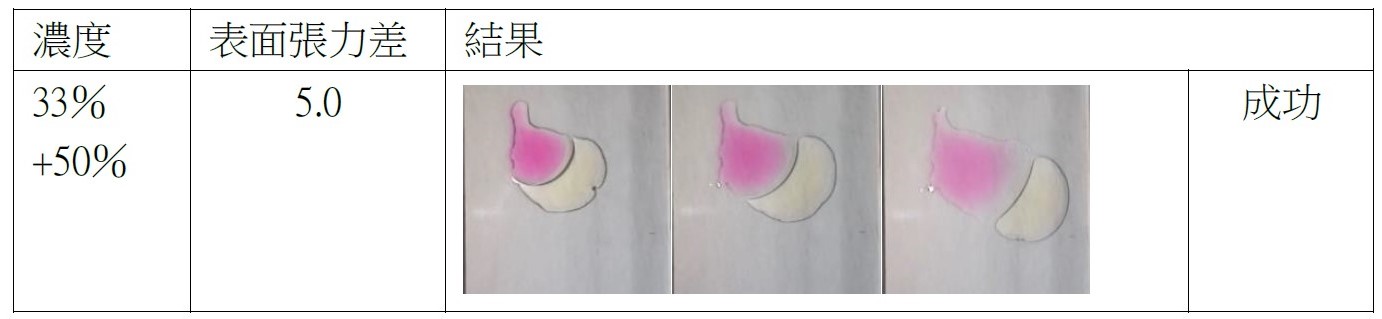

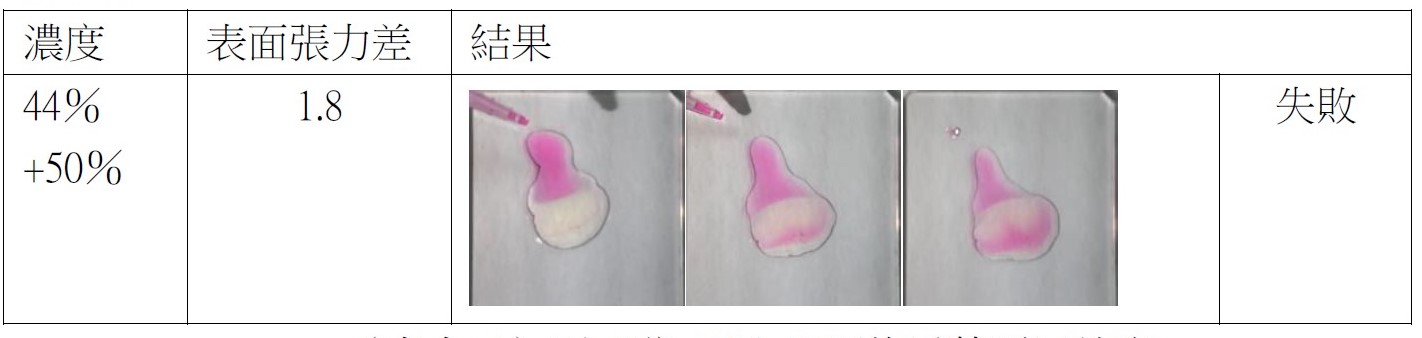
設計被動選色(sorting experiment,或稱階梯實驗)之機制

探討溶液混合或停止追逐現象之成因

討論
載玻片的前置處理

探討產生馬蘭哥尼效應的條件
探討存在最小表面張力差的原因
決定欲使用的丙二醇濃度
如何決定以階梯式操作此實驗

結論
參考資料